"AHH, WHAT A FINE DAY... FOR SCIENCE."
-Dexter, Dexter's Lab
-Dexter, Dexter's Lab
NOTES FOR--
discussing pitch, octaves, harmonics and overtones in relation to sound waves/wavelenghts, and the scientific/mathematic aspects of harmonic oscillators, including actual musical equations (both tangible and functional!).
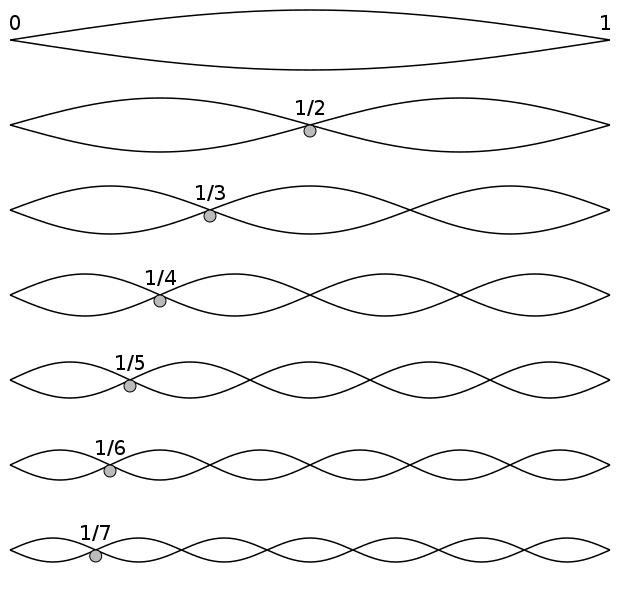
visualize a vibrating string.
-"nodes" (fixed points at the ends)
[demonstration:
using a xylophone key]
-create nodes with fingered notes
-harmonics divide up the string into (fractional) sections. each point creates a higher pitch of an already higher note. ("equal-sized sections resonating at increasingly higher frequencies."-wiki)
-harmonics and octaves; all based on multiples. create a node: the sound created will be the same tone as its harmonic, but the harmonic may be octaves higher depending on the instrument.
-fundamental frequency= lowest vibrating note. this is the one we hear primarily, amidst the range of harmonics (octaves as well as non octaves) that are actually there (overtones).
IMPRECISE DIVISIONS CAUSING EVEN THE SLIGHTEST INACCURACY MERELY INTERFERE WITH THE TRAVELING OF THE SOUND WAVES.
-explain how sound stops
"The harmonic series is an arithmetic series (1×f, 2×f, 3×f, 4×f, 5×f, ...). In terms of frequency (measured in cycles per second, or hertz (Hz) where f is the fundamental frequency), the difference between consecutive harmonics is therefore constant and equal to the fundamental. But because our ears respond to sound nonlinearly, we perceive higher harmonics as "closer together" than lower ones. On the other hand, the octave series is a geometric progression (2×f, 4×f, 8×f, 16×f, ...), and we hear these distances as "the same" in the sense of musical interval. In terms of what we hear, each octave in the harmonic series is divided into increasingly "smaller" and more numerous intervals." -Wikipedia
^I'll explain this verbally and with visual aid~ (:

